Comparing Amazon Halo to Apple Watch
The Amazon Halo is a new fitness band with a few interesting features, notably a body scan option that claims to be more accurate than a household scale at calculating body fat. I’ll look in depth at that feature later, but meanwhile I wanted a quick-and-dirty test of the overall sensor accuracy.
To help with the analysis, I created a new R package called amazonhalor that can read the raw data you can download from the Halo.
devtools::install_github("richardsprague/amazonhalor")The Halo data files are a little quirky, so this package offers a number of convenience functions to automatically convert the raw data into an R dataframe that’s a bit easier to handle.
My Apple Watch data is stored in the variable watch_data_full, so I’ll use the package to read data from Halo so I can compare.
If you set the variable halo_directory to a pathname pointing to the Amazon Health Data directory, read the Halo heart rate data like this:
halo_heartrate_df <- amazonhalor::halo_heartrate_df(halo_directory)
halo_activity_daily_df <- amazonhalor::halo_daily_df(halo_directory)
halo_sleep_df <- amazonhalor::halo_sleep_sessions_df(halo_directory)Sleep
Unlike the Apple Watch with its power-hungry display, the Halo battery easily lasts a full two days without charging, making it a worthwhile sleep tracker. Unlike my Apple Watch, Halo samples my skin temperature as well, giving it another parameter of sleep quality.
In general I’m finding the Halo to be pretty accurate about sleep. With no intervention from me, it accurately identifies precisely when I fall asleep and when I wake up. My “morning feel” – how refreshed I feel upon getting up – matches pretty well with the Halo “Sleep Quality” score. In this Halo does better than the Autosleep app I’ve long used with my Apple Watch.
halo_sleep_df %>% pivot_longer(cols = c("Z","REM", "Deep", "Light"), names_to = "Phase", values_to = "Duration") %>%
transmute(date = `Date Of Sleep`, Phase = factor(Phase), Duration) %>% dplyr::filter(Phase != "Z") %>%
ggplot(aes(x=date, y = Duration/3600, fill = Phase)) + geom_col() +
labs(title = "Sleep Duration", subtitle = "Amazon Halo", y = "Hours", x = "") +
scale_x_date(date_breaks = "1 week", date_labels = "%b-%d") +
theme(axis.text.x = element_text(angle = 90, hjust = 1))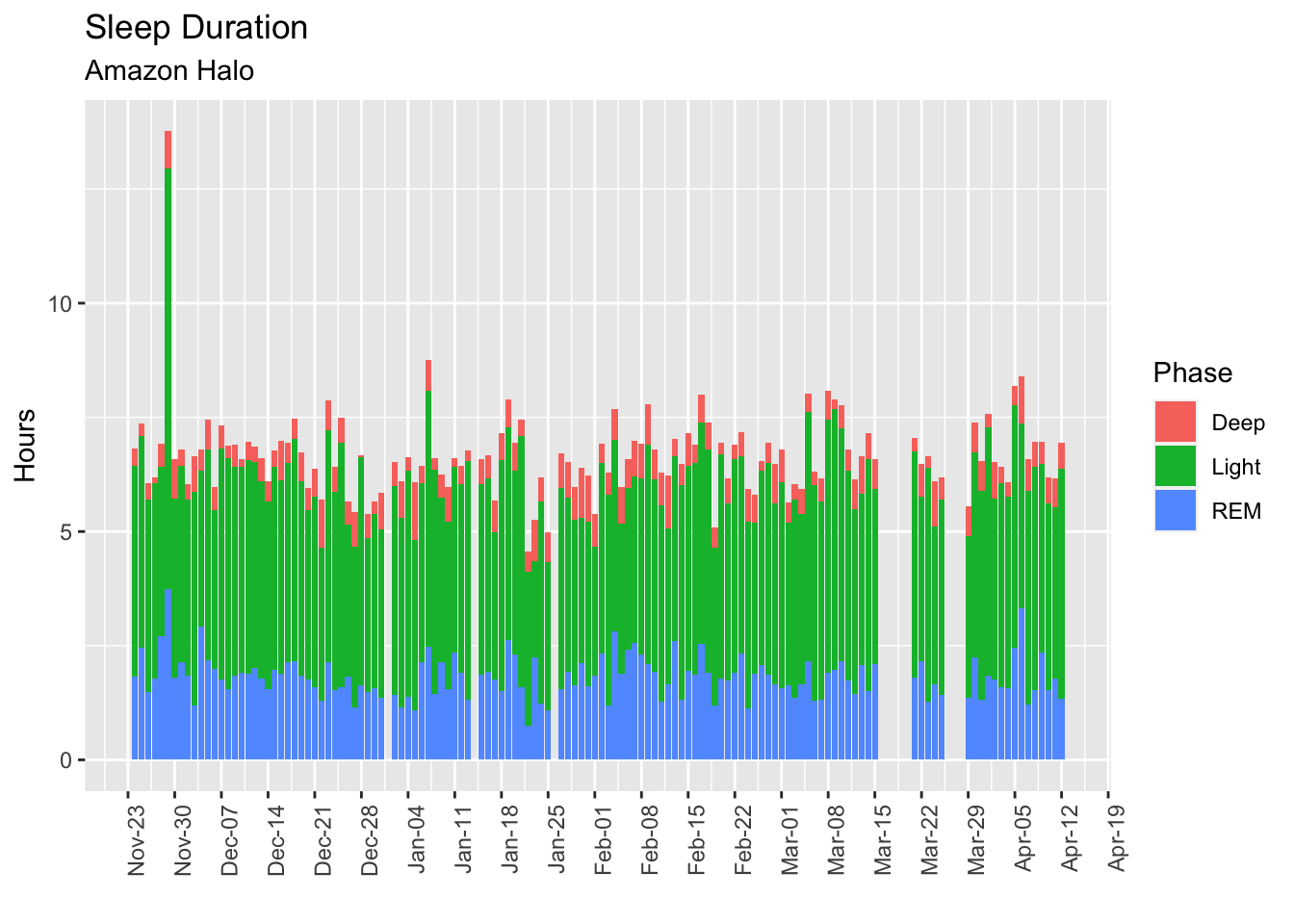
Note my lack of time spent in deep sleep, consistent with what I’ve seen with all other sleep gadgets I’ve tried.
Resting Heart Rate
Apple Watch and Halo seem quite different in their measurement of resting heart rate:
watch_halo <- watch_data_full %>% dplyr::filter(endDate >= "2020-11-23" & type=="RestingHeartRate") %>%
transmute(Date=lubridate::as_date(endDate, tz = Sys.timezone()),sourceName=sourceName,`Resting Heart Rate (bpm)`=value) %>%
full_join(select(halo_activity_daily_df, Date, sourceName, `Resting Heart Rate (bpm)`)) %>%
transmute(Date = Date, HR = `Resting Heart Rate (bpm)`, source = factor(sourceName, labels = c("Amazon Halo", "Apple Watch")))
a <- watch_halo %>% pivot_wider(names_from = source, values_from = HR, values_fn = function(x) x[1]) %>% bind_cols(x = .[2] - .[3])
names(a) <- c("Date","Apple Watch", "Amazon Halo", "Diff")
p1 <- watch_halo %>%
ggplot(aes(x=Date, y= HR, color = source)) +
geom_line( size=2) + # data = filter(watch_halo, source != "Diff"),
labs(title = "", color = "Source", x = "") +
scale_x_date(date_breaks = "1 week", date_labels = "%b-%d") +
theme(axis.text.x = element_blank(),
axis.ticks = element_blank())
p2 <- a %>% ggplot(aes(x=Date, y=Diff)) + geom_col() +
labs(title = "", color = "Source", x = "", y = "Watch HR - Halo HR") +
scale_x_date(date_breaks = "1 week", date_labels = "%b-%d") +
theme(axis.text.x = element_text(angle = 90, hjust = 1))
library(patchwork)
patchwork <- p1 / p2
patchwork + plot_annotation(title = "Apple Watch vs. Amazon Halo",
subtitle = "Resting Heart Rate Compared",
theme = theme(plot.title = element_text(size = 25)))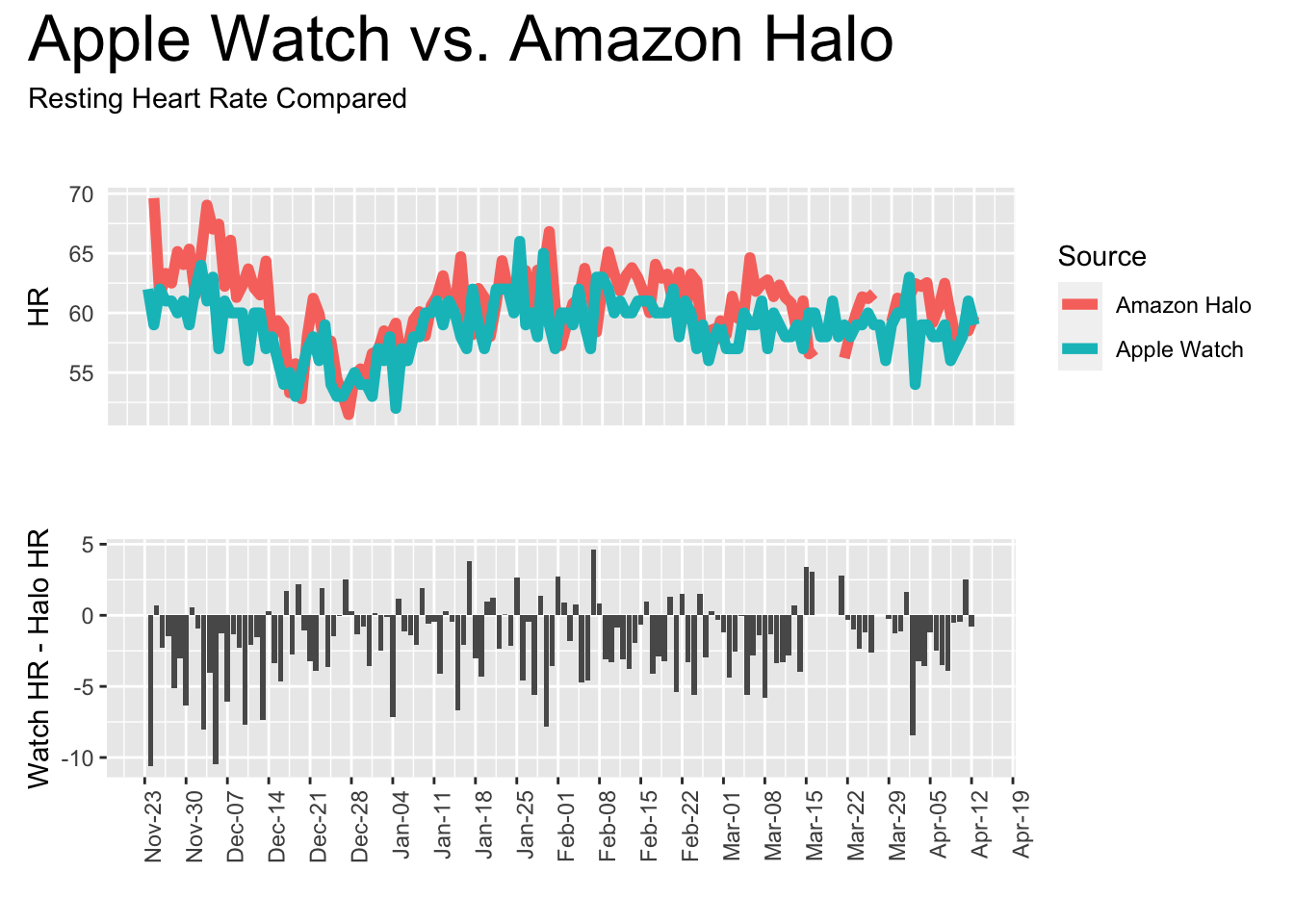
Resting heart rate values appear wildly different at the beginning of this series but they seem to converge after a month or two of use. Is the Halo “learning” something about me?
That chart was made using the daily summary, which comes from an algorithm that each manufacturer uses to compute what they think is your resting heart rate for the day. I’m not sure exactly how this is computed, which may explain the variance.
Heart Rates
How about the actual heart rates throughout the day? Because we’re looking at raw heart rate data, I assume it’s much closer to the truth, assuming each device accurately measures and stores my minute-by-minute heart rate.
library(tidyverse)
library(lubridate)
hr_compare <- watch_data_full %>% dplyr::filter(endDate >= "2021-02-12" & type=="HeartRate") %>%
transmute(datetime=lubridate::as_datetime(endDate,
tz = Sys.timezone()),
sourceName=sourceName,
value=value) %>%
full_join(select(halo_heartrate_df %>% sample_frac(0.03), datetime, sourceName, value)) %>%
mutate(source = factor(sourceName, labels = c("Amazon Halo", "Apple Watch")))
hr_compare %>% dplyr::filter(datetime>"2021-02-12 12:00pm") %>%
ggplot(aes(x=datetime, y = value, color = source)) + geom_point() + geom_smooth(method = "loess") +
labs(title = "Apple Watch vs. Halo", color = "Source",
x = "",
y = "Heart Rate (bpm)")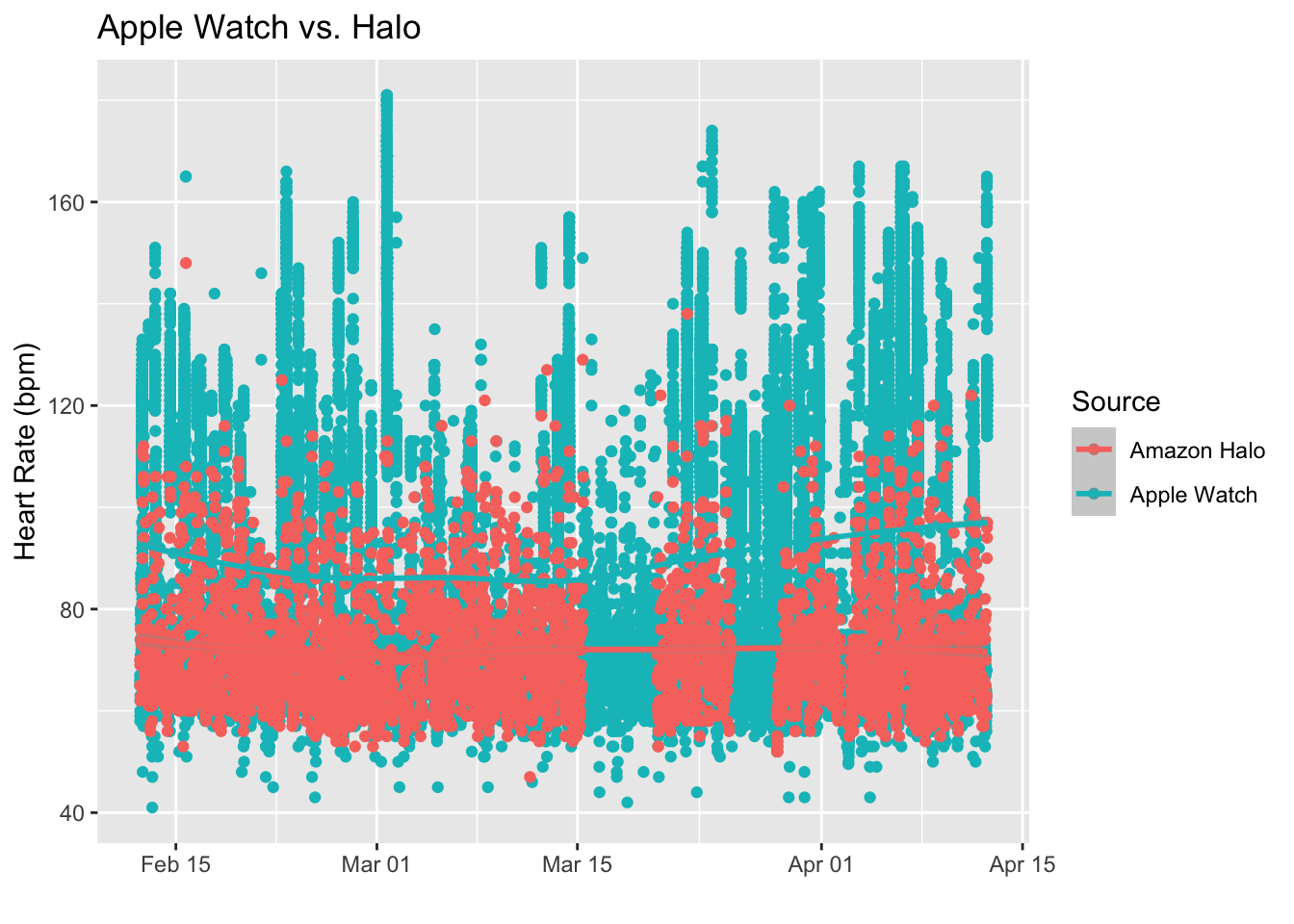
The differences are huge, especially when I’m exercising at higher heart rates. Apple Watch correctly indicates numbers well above 120 or 150 or beyond when I feel I’m pushing myself to my limit, while Halo rarely gives me more than 115 beats per minute no matter how hard I try. There’s clearly something wrong with the Halo workout calculations.
Biggest problem with #amazonhalo is it doesn't register heartrate > 110 bpm or so, even in the heaviest workout. Must be a bug, because no way am I in this good shape. pic.twitter.com/OTb2kPpRPi
— Richard Sprague (@sprague) December 9, 2020
Body Fat
Halo claims to be more accurate than a bathroom scale at measuring overall body fat.
amazonhalor::halo_body_df(halo_directory) %>%
ggplot(aes(x=Timestamp, y = Fat_Percentage)) +
geom_line() +
geom_point(color = "red") +
labs(title = "My Body Fat",
y = "Fat Percentage") +
theme(axis.text.x = element_text(angle = 90, hjust = 1),
axis.title.x = element_blank())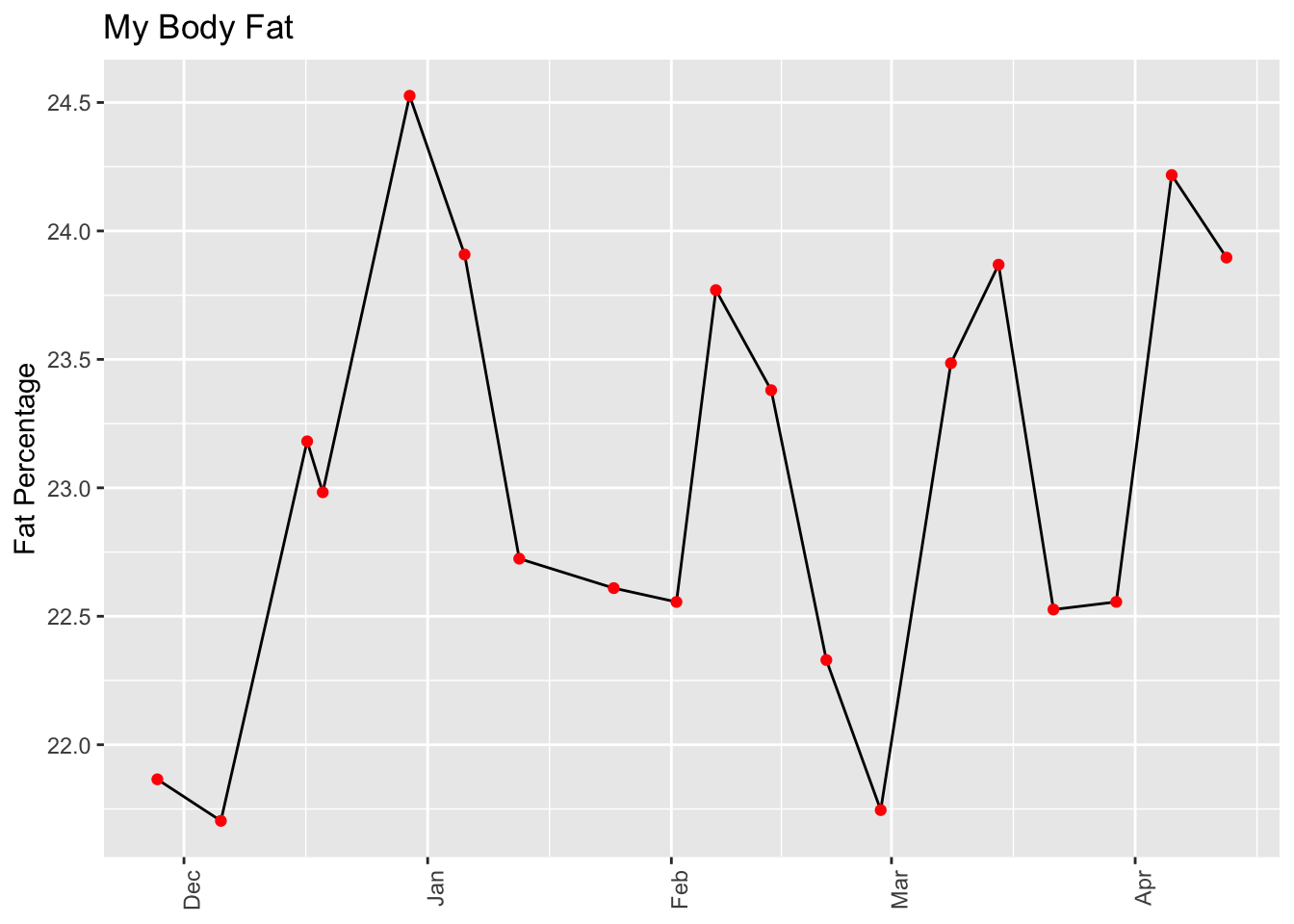
I’ve not done a serious clinical-grade body composition measurement (like the one you can get from Dexa Scan), so I don’t know whether the absolute values here are correct. But for a lean guy like me, the absolute values seem roughly correct, climbing during the Christmas eating season, and then dropping. I’m not sure if that early-February rise was due to something in particular – I didn’t notice any weight difference more than a pound or two. I’ll keep measuring regularly to see if there are other patterns.
Tone
One feature that gets too much attention is the conversation “tone” measurement that uses the Halo’s built-in microphone to analyze your speech throughout the day in an attempt to find patterns.
halo_tone_utterances_df <- amazonhalor::halo_tone_utterances_df(halo_directory)
p <- halo_tone_utterances_df %>% dplyr::filter(StartTime >= today() - days(3)) %>%
pivot_longer(cols = c("Positivity","Energy"),
names_to = "Measure",
values_to = "Intensity") %>%
ggplot(aes(x=StartTime, y = Intensity, color = Measure)) + geom_point() +
labs(title = "Amazon Halo Tone Measurements", x = "")
library(gganimate)
anim <- p + geom_point(aes(color = Measure, group = 1L)) + transition_states(Measure, transition_length = 2, state_length = 1)
anim + ease_aes('cubic-in-out')
I’m not sure how to interpret this, but it sure is cool to make the plots!
Statistics
Finally, a few technical metrics. I realize this isn’t a good analysis, but it’s my initial attempt to decipher exactly where the two bands are different. Results from the two bands diverge most at higher heart rates, where it appears that Halo is simply not measuring as well as Apple Watch.
with(hr_compare, table(source))## source
## Amazon Halo Apple Watch
## 10685 37767hr_compare %>% group_by(source) %>% summarise(q1 = quantile(value, .25),
q2 = quantile(value, 0.75)) %>%
knitr::kable(col.names = c("Device", "HR Q1", "HR Q2"), caption = "Heart Rate by Quartile")| Device | HR Q1 | HR Q2 |
|---|---|---|
| Amazon Halo | 64 | 78 |
| Apple Watch | 67 | 109 |
hr_compare %>% split(.$source) %>% purrr::map(summary)## $`Amazon Halo`
## datetime sourceName value
## Min. :2020-11-23 14:31:47 Length:10685 Min. : 45.00
## 1st Qu.:2020-12-26 06:08:28 Class :character 1st Qu.: 64.00
## Median :2021-01-30 03:20:32 Mode :character Median : 69.00
## Mean :2021-01-29 21:30:26 Mean : 72.38
## 3rd Qu.:2021-03-03 08:55:20 3rd Qu.: 78.00
## Max. :2021-04-12 12:55:58 Max. :160.00
## source
## Amazon Halo:10685
## Apple Watch: 0
##
##
##
##
##
## $`Apple Watch`
## datetime sourceName value
## Min. :2021-02-12 00:06:51 Length:37767 Min. : 41.00
## 1st Qu.:2021-02-24 03:16:51 Class :character 1st Qu.: 67.00
## Median :2021-03-14 09:29:51 Mode :character Median : 85.00
## Mean :2021-03-13 23:01:27 Mean : 90.12
## 3rd Qu.:2021-03-30 17:19:51 3rd Qu.:109.00
## Max. :2021-04-12 12:42:51 Max. :181.00
## source
## Amazon Halo: 0
## Apple Watch:37767
##
##
##
## t.test(hr_compare %>% dplyr::filter(source=="Apple Watch") %>% pull(value),
hr_compare %>% dplyr::filter(source=="Amazon Halo") %>% pull(value))##
## Welch Two Sample t-test
##
## data: hr_compare %>% dplyr::filter(source == "Apple Watch") %>% pull(value) and hr_compare %>% dplyr::filter(source == "Amazon Halo") %>% pull(value)
## t = 99.631, df = 35183, p-value < 2.2e-16
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## 17.39186 18.08989
## sample estimates:
## mean of x mean of y
## 90.12206 72.38119Conclusion: the two device don’t agree on heart rates, though I’m unsure how much of this is software and how much is due to limitations (or bugs) in the hardware. I’ll continue to explore and update this post when I get more answers.